K-means聚类算法概述
K-means聚类算法是一种广泛应用于数据科学和商业领域的无监督机器学习方法。它通过将数据点划分为K个簇,使得每个簇内的数据点尽可能相似,而不同簇之间的数据点尽可能不同。本文将详细介绍K-means聚类算法的工作原理、步骤以及评估方法,特别强调Elbow Method在确定最佳聚类数中的重要性。
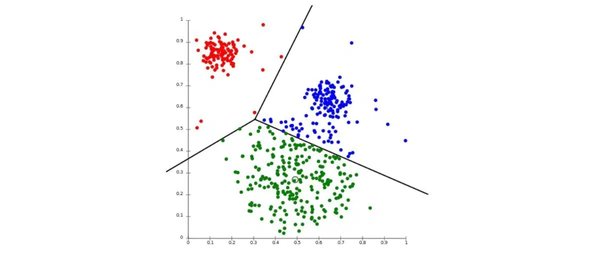

K-means聚类算法的工作原理
K-means聚类算法的工作原理可以分为以下几个步骤:
- 初始化:随机选择K个数据点作为初始的聚类中心。
- 分配:将每个数据点分配到距离最近的聚类中心所在的簇。
- 更新:重新计算每个簇的聚类中心,即簇内所有数据点的平均值。
- 迭代:重复步骤2和步骤3,直到聚类中心不再发生变化或达到预定的迭代次数。
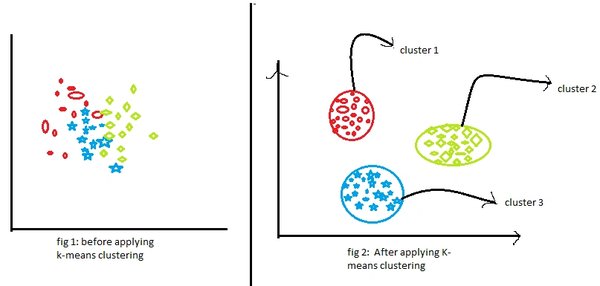

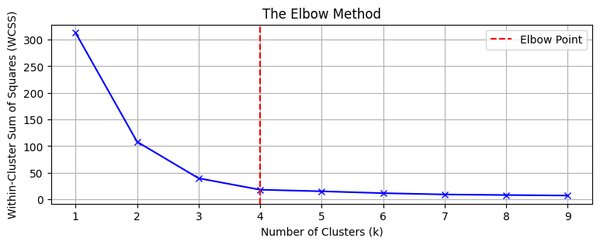
Elbow Method:确定最佳聚类数
在K-means聚类算法中,选择合适的K值是一个关键问题。Elbow Method是一种常用的方法,用于确定最佳聚类数。其基本思想是绘制K值与聚类误差(如SSE,Sum of Squared Errors)之间的关系图,寻找“肘部”点,即误差下降速度明显减缓的点。
Elbow Method的步骤
- 计算SSE:对于不同的K值,计算聚类误差SSE。
- 绘制图形:将K值与对应的SSE绘制成图形。
- 寻找肘部:在图形中寻找SSE下降速度明显减缓的点,该点即为最佳K值。
Elbow Method的优缺点
- 优点:简单直观,易于理解和实现。
- 缺点:在某些情况下,肘部点不明显,需要结合其他方法进行判断。

K-means聚类算法的应用
K-means聚类算法在数据科学和商业领域有着广泛的应用,例如:
- 客户细分:通过聚类分析,将客户划分为不同的群体,以便制定针对性的营销策略。
- 图像分割:将图像中的像素点进行聚类,实现图像的分割和识别。
- 异常检测:通过聚类分析,识别数据中的异常点或离群点。
总结
K-means聚类算法是一种强大且灵活的工具,能够帮助我们从复杂的数据中提取有价值的信息。通过Elbow Method,我们可以更准确地选择最佳聚类数,从而提高聚类的效果。随着数据科学和商业分析的不断发展,K-means聚类算法将在更多领域发挥重要作用。
“`markdown
| 步骤 | 描述 |
|---|---|
| 初始化 | 随机选择K个数据点作为初始的聚类中心 |
| 分配 | 将每个数据点分配到距离最近的聚类中心所在的簇 |
| 更新 | 重新计算每个簇的聚类中心,即簇内所有数据点的平均值 |
| 迭代 | 重复步骤2和步骤3,直到聚类中心不再发生变化或达到预定的迭代次数 |
“`
通过本文的介绍,相信读者对K-means聚类算法及其应用有了更深入的理解。在实际应用中,结合Elbow Method等评估方法,可以更好地发挥K-means聚类算法的潜力。
© 版权声明
文章版权归作者所有,未经允许请勿转载。
相关文章
暂无评论...
