
遗传算法简介
遗传算法(Genetic Algorithm, GA)是一种模拟自然选择和遗传机制的优化算法,广泛应用于解决复杂优化问题。其核心思想是通过模拟生物进化过程,不断迭代优化种群中的个体,以找到问题的最优解。


关键参数设置与优化
种群规模
种群规模是遗传算法中的一个重要参数。较大的种群可以提供更广泛的探索空间,有助于找到全局最优解;然而,过大的种群也会增加计算成本。通常建议基于问题复杂度来决定合适的种群数量,实践中30至100之间的范围是一个常见的选择。
交叉率
交叉率(Crossover Fraction)是影响遗传算法性能的另一个关键参数。较高的交叉率能够促进基因间的交流,从而加速收敛速度;但同时也可能导致早熟现象,即快速陷入局部最优点附近无法跳出。一般推荐初始设为约70%-90%之间,并视情况动态调整。
变异几率
变异几率(Mutation Rate)用于防止种群多样性丧失,进而避免算法停滞不前。较低的水平(如0.1%)足以维持必要的随机扰动,而不破坏已经形成的优良模式结构。
自适应机制
为了进一步提高性能表现,可考虑采用自适应机制自动修改上述提到的各项系数。例如,随着迭代次数增多逐渐降低交叉比率,以减少后期不必要的大幅度跳跃变化;或是依据当前最佳个体与其他成员间差异程度,灵活控制突变频率等措施,均能有效增强鲁棒性。
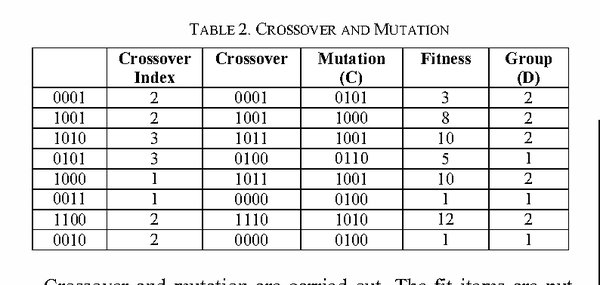

0-1背包问题的应用
0-1背包问题是一个经典的组合优化问题,目标是在不超过背包最大容量的前提下,选择装入的物品,使得背包中物品的总价值最大。遗传算法在该问题中的应用,通过编码、选择、交叉和变异等操作,能够高效地找到近似最优解。
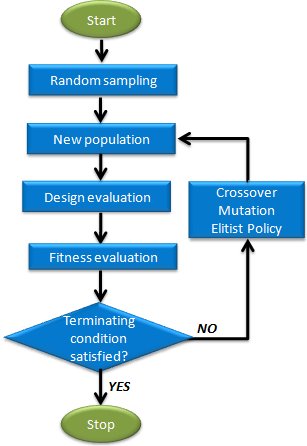
实现步骤
- 编码:将每个物品的选择状态(装入或不装入)编码为二进制串。
- 初始化种群:随机生成一定数量的初始解。
- 适应度评估:计算每个个体的适应度值,即背包中物品的总价值。
- 选择:根据适应度值选择优秀的个体进行繁殖。
- 交叉:通过交叉操作生成新的个体。
- 变异:对部分个体进行变异操作,以增加种群的多样性。
- 迭代:重复上述步骤,直到满足终止条件。
结论
遗传算法通过合理的参数设置和优化策略,能够有效解决复杂的优化问题,如0-1背包问题。通过引入自适应机制和动态调整策略,可以进一步提升算法性能,为实际应用提供高效、可靠的解决方案。
| 参数 | 推荐值 | 说明 |
|---|---|---|
| 种群规模 | 30-100 | 基于问题复杂度决定 |
| 交叉率 | 70%-90% | 初始设定,可动态调整 |
| 变异几率 | 0.1% | 维持必要的随机扰动 |
| 自适应机制 | 动态调整 | 根据迭代次数和个体差异灵活控制 |
通过上述方法和策略,遗传算法在解决复杂优化问题时表现出色,为实际应用提供了强有力的工具。
