引言
在人工智能(AI)领域,损失函数是模型训练的核心组成部分,它直接决定了模型的优化方向和最终性能。随着AI技术的不断发展,传统的损失函数逐渐暴露出其在复杂任务中的局限性。为此,研究人员提出了“终极损失函数”这一新概念,旨在通过更精细的损失设计,提升模型的推理能力和泛化性能。
传统损失函数的局限性
传统的损失函数,如均方误差(MSE)和交叉熵损失,虽然在许多任务中表现出色,但在处理复杂、非线性的数据分布时,往往显得力不从心。例如,在金融时间序列预测中,传统的MSE和MAE指标无法全面评估模型在实际应用中的表现,忽略了时间相关性和非平稳性下的稳健性。
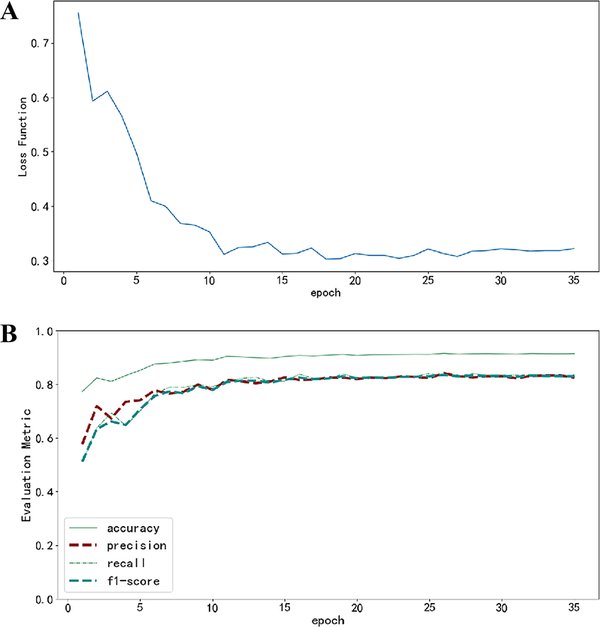
终极损失函数的设计理念
终极损失函数的设计理念在于通过多维度的损失计算,全面评估模型的性能。以FinTSBridge框架为例,其引入了msIC(平均序列相关性)和msIR(相关性稳定性比率)两个新的评估指标,分别衡量预测时间序列的真值和预测值之间的相关系数,以及模型在不同样本中的相关性稳定性。
msIC与msIR的计算公式
-
msIC:衡量预测时间序列的真值和预测值之间的相关系数,计算公式为:
[
msIC = \frac{1}{B \times C} \sum{i=1}^{B} \sum{j=1}^{C} \text{corr}(Y{ij}, \hat{Y}{ij})
]
其中,(Y{ij})和(\hat{Y}{ij})分别表示第(i)个样本和第(j)个变量的真实值和预测值。 -
msIR:衡量模型实现的有效相关性与时间序列动态变化所引起的相关性“噪声”之间的比率,计算公式为:
[
msIR = \frac{msIC}{\sigma(msIC)}
]
其中,(\sigma(msIC))表示msIC序列的标准差。
终极损失函数在AI模型中的应用
终极损失函数在AI模型中的应用不仅限于金融领域,其在自然语言处理、计算机视觉等多个领域也展现出了强大的潜力。例如,在DeepSeek的R1模型中,通过引入MoE(混合专家)架构和MLA(多头潜在注意力机制),终极损失函数显著提升了模型的推理效率和预测能力。
MoE架构的优势
MoE架构通过将复杂的AI模型分解为多个子模型,实现了高效的推理和训练。在DeepSeek的R1模型中,MoE架构的应用使得模型在推理过程中仅激活相关领域的专家,从而大幅降低了计算资源的消耗。
MLA机制的创新
MLA机制通过将注意力头的键和值进行线性变换,压缩到一个共享的低维潜在向量空间,进一步提升了模型的推理效率。在DeepSeek的R1模型中,MLA机制的应用使得模型在处理长文本和复杂推理任务时,表现出更高的准确性和稳定性。
终极损失函数的未来展望
终极损失函数的提出为AI模型的优化提供了新的思路。随着AI技术的不断发展,终极损失函数有望在更多领域得到应用,推动AI模型的性能提升和应用拓展。例如,在医疗诊断、自动驾驶等领域,终极损失函数可以通过更精细的损失设计,提升模型的准确性和鲁棒性。
结论
终极损失函数作为AI模型优化的新范式,通过多维度的损失计算和精细的模型设计,显著提升了模型的推理能力和泛化性能。随着AI技术的不断发展,终极损失函数有望在更多领域得到应用,推动AI模型的性能提升和应用拓展。
