图论与图学习的基础概念
图论是数学的一个分支,专注于研究图的结构和性质。图由节点(顶点)和边组成,用于表示对象及其相互关系。随着机器学习的发展,图学习(Graph Learning)逐渐成为热门领域,将图论与机器学习相结合,解决复杂问题。
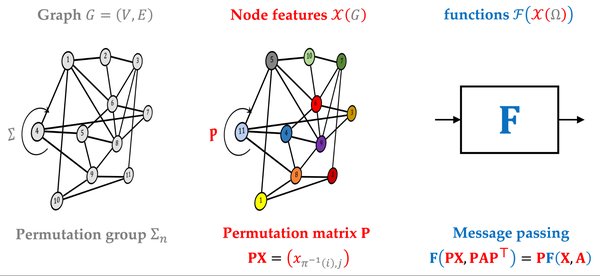

图论在机器学习中的应用
图论在机器学习中的应用广泛且深入,以下是几个典型的应用场景:
社交网络结构分析
社交网络可以抽象为图,其中节点代表用户,边代表用户之间的关系。通过图论算法,可以分析社交网络中的社区结构、关键节点(如意见领袖)以及信息传播路径。
欺诈检测
在金融领域,图论被用于检测欺诈行为。通过构建交易网络,分析异常交易模式,识别潜在的欺诈团伙。
消费者行为理解
电商平台可以利用图论分析用户的购买行为和偏好。例如,通过构建用户-商品图,推荐系统可以更精准地预测用户需求。
实时推荐系统
图论在推荐系统中也发挥着重要作用。通过分析用户与商品之间的交互图,可以实时生成个性化推荐,提升用户体验。
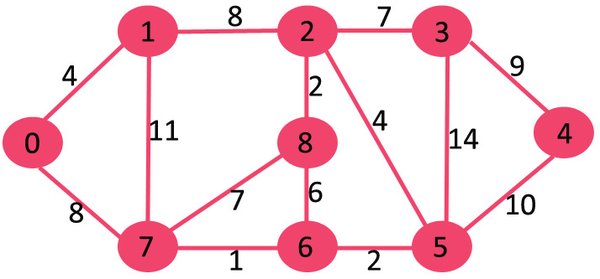

图论中的核心算法
图论中涉及多种算法,以下是几个关键算法的介绍:
寻路算法
寻路算法用于在图中找到从一个节点到另一个节点的路径。常见的寻路算法包括深度优先搜索(DFS)和广度优先搜索(BFS)。
最短路径计算
最短路径算法用于找到两个节点之间的最短路径。Dijkstra算法是最经典的最短路径算法之一,适用于带权图。
聚类程度度量
聚类程度用于衡量图中节点的聚集程度。例如,社交网络中的社区检测可以通过聚类算法实现。
中心度分析
中心度用于衡量节点在图中的重要性。常见的中心度指标包括度中心性、接近中心性和介数中心性。
图学习的前沿与挑战
图学习结合了图论和机器学习,能够处理复杂的非欧几里得数据。然而,图学习也面临一些挑战,例如图数据的稀疏性、动态性以及计算复杂度。
总结
图论与图学习为机器学习提供了强大的工具,能够解决社交网络分析、欺诈检测、消费者行为理解等实际问题。通过掌握寻路算法、最短路径计算、聚类程度度量等核心概念,数据科学家可以更好地应用图论解决现实问题。未来,随着技术的发展,图学习将在更多领域展现其价值。
