多波动率并行模型在金融量化中的应用与优化

多波动率并行模型的理论基础

多波动率并行模型，特别是Heston模型，在金融量化领域中占据了重要地位。Heston模型通过引入随机波动率，改进了传统Black-Scholes模型中波动率恒定的假设。Heston模型的核心在于其波动率过程是一个均值回归的随机过程，这使得资产价格在模型下呈现出受限的特征，与Black-Scholes模型中价格持续扩散的情况形成鲜明对比。

Heston模型与传统模型的差异

Heston模型的一个重要特征是波动率与回报的相关性决定了回报分布的偏度和峰度。这种相关性在Black-Scholes模型中是不存在的，因为后者的波动率是恒定的。因此，Heston模型在对同一执行价格和标的资产进行定价时，往往会产生与Black-Scholes模型不同的结果。这种差异在实际应用中具有重要意义，特别是在奇异期权的定价和风险管理中。

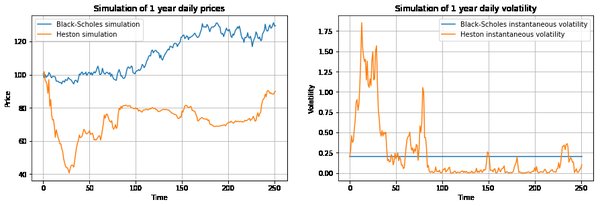
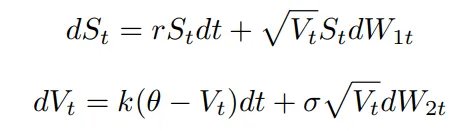
多波动率并行模型的实践应用

在实际应用中，Heston模型的复杂性使得其解析解难以获得，因此数值解成为主要的解决方案。蒙地卡罗模拟法在这一过程中发挥了重要作用，尤其是在处理复杂的结构商品时。通过多核CPU和GPU的并行运算技术，可以显著提高模拟的效率，从而满足实务操作的需求。

Python在金融量化中的优化

Python作为一种强大的编程语言，在金融量化代码的编写中展现了其独特的优势。通过优化算法和数学应用，Python能够有效地处理复杂的金融数据，并实现股票价格特征的自动标注功能。此外，Python在多隐层神经网络的优化技术中也展现了其应用数学的实践性和艺术性，为金融量化提供了新的视角和工具。

结论

多波动率并行模型，特别是Heston模型，在金融量化中的应用不仅提高了定价的准确性，还为风险管理提供了新的工具。Python的优化算法和数学应用进一步增强了这些模型的实际操作性，使得金融量化分析更加高效和精确。未来，随着计算技术的不断发展，多波动率并行模型在金融领域的应用将会更加广泛和深入。