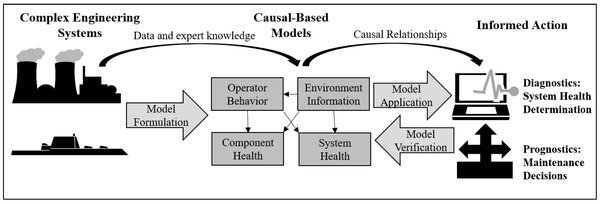
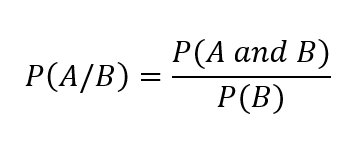引言
贝叶斯网络(Bayesian Network)是一种概率图模型,由Judea Pearl在1985年首先提出,用于模拟人类推理过程中因果关系的不确定性处理模型。它在多个领域中得到广泛应用,如医疗诊断、故障诊断、推荐系统、生物信息学、自然语言处理、机器学习等。本文将从基础概念、结构学习、参数估计到实际应用,全方位解析贝叶斯网络的原理及其在多个领域中的广泛应用。
基础概念
贝叶斯定理
贝叶斯定理是贝叶斯网络的核心,允许我们在已知某些证据的情况下更新我们的概率估计。贝叶斯定理的公式为:
$$
P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)}
$$
其中,$P(A|B)$ 是后验概率,$P(B|A)$ 是似然,$P(A)$ 是先验概率,$P(B)$ 是边缘概率。
条件独立性
条件独立性是贝叶斯网络中的一个重要概念。如果两个变量在已知某个条件后变得无关,就叫条件独立。例如,在已知学习时间的情况下,课程难度对成绩的影响可以忽略不计。
结构学习
基于约束的方法
基于约束的方法利用条件独立性测试(Conditional Independence, CI)来学习贝叶斯网络结构,尽可能多地去除变量之间的多余的依赖关系。然而,这种方法需要大量样本来测试独立性,时间代价较大。
基于评分搜索的方法
基于评分搜索的方法是目前应用最广泛的结构学习方法。它利用评分函数来评估每个可能的网络结构是否优秀。然而,随着节点数量的增加,搜索代价过高。
混合方法
混合方法结合了基于约束和基于评分搜索的方法,通过独立性检验缩小搜索空间,然后再采用基于评分搜索的方式学习最优的网络。
参数估计
最大似然估计(MLE)
最大似然估计是一种简单的参数估计方法,直接用数据中的频率作为概率。例如,如果课程难度高时80%的学生选择长时间学习,MLE会直接估计学习时间长的概率为80%。
期望最大化算法(EM)
EM算法用于处理存在隐变量或数据缺失时的参数估计问题。它通过迭代步骤更新参数,直到模型收敛。
贝叶斯估计
贝叶斯估计通过引入先验分布,结合观测数据计算后验分布,从而估计参数。它比MLE更适用于数据量小或存在稀疏数据的情况。
实际应用
医疗诊断
贝叶斯网络在医疗诊断中广泛应用,通过模拟疾病与症状之间的因果关系,帮助医生进行更准确的诊断。
故障诊断
在航空航天领域,贝叶斯网络用于故障诊断系统,通过明确每个报警信号的产生逻辑,提高系统的可靠性。
推荐系统
贝叶斯网络在推荐系统中也有应用,通过模拟用户与物品之间的因果关系,提供个性化的推荐。
生物信息学
在生物信息学中,贝叶斯网络用于基因表达数据的分析,帮助研究人员理解基因之间的相互作用。
自然语言处理
在自然语言处理中,贝叶斯网络用于语言模型的构建,通过模拟词语之间的因果关系,提高语言生成的质量。
总结
贝叶斯网络是一种强大的概率图模型,能够模拟人类推理过程中因果关系的不确定性处理模型。它在多个领域中得到广泛应用,如医疗诊断、故障诊断、推荐系统、生物信息学、自然语言处理、机器学习等。通过理解贝叶斯网络的基础概念、结构学习、参数估计和实际应用,我们可以更好地利用这一工具解决复杂的实际问题。