三维动态平衡方程的理论基础
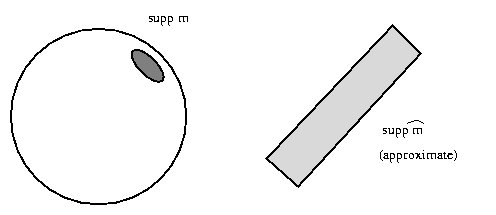
三维动态平衡方程在数学和物理学中占据着核心地位,尤其是在几何测度论和调和分析领域。挂谷猜想的突破,由华人数学家王虹及其合作者完成,不仅解决了百年难题,还为三维动态平衡方程的研究提供了新的视角和方法。挂谷猜想最初由日本数学家挂谷宗一在1917年提出,探讨了在三维空间中旋转单位线段所需的最小区域。王虹的研究通过创新性地构建δ管集合理论,证实了三维Kakeya集合的Hausdorff维度必为3,这一成果不仅填补了理论空白,更为高维推广提供了新工具。

挂谷猜想的跨学科影响
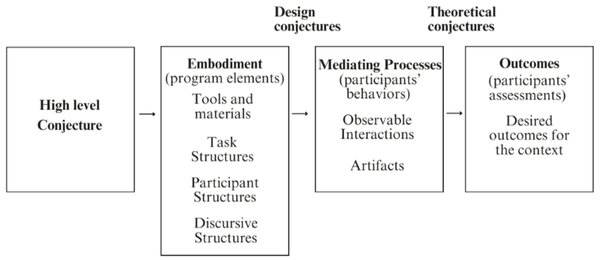
挂谷猜想的解决不仅对几何测度论有重要意义,还在调和分析、偏微分方程和数论等领域产生了深远影响。例如,在调和分析中,挂谷猜想与傅里叶变换限制问题密切相关,而在物理中,它影响了波动方程的建模。此外,挂谷猜想的研究技术,如解耦方法,甚至推动了数论中整数幂和表示问题的突破。这些跨学科的应用展示了三维动态平衡方程在连接不同数学分支中的关键作用。


三维动态平衡方程在流体力学中的应用
在流体力学中,三维Navier-Stokes方程是描述不可压缩流体运动的核心方程。通过有限差分法、谱方法或有限元方法,研究人员可以在Matlab环境中对三维Navier-Stokes方程进行数值求解。特别是基于压力泊松方程的投影方法,能够有效地分离速度场和压力场的计算,保持质量守恒条件下的动量平衡。这种方法在处理复杂流体动力学问题时表现出色,为工程和科学研究提供了重要工具。
三维动态平衡方程在地球物理中的应用
在地球物理领域,三维密度反演是理解地下结构的关键技术。传统方法通过增加网格数量来提高复杂地质体的拟合度,但会降低反演效率并增加非唯一性。新提出的自适应网格划分方法,结合边缘特征和相关成像约束,能够显著提高反演结果的精度和计算效率。这种方法在澳大利亚奥林匹克坝地区的实际应用中,成功验证了其正确性和有效性,为地质勘探提供了新的解决方案。
三维动态平衡方程在拓扑优化中的应用
在拓扑优化中,伴随变量法是一种高效的灵敏度分析方法,特别适用于设计变量数量庞大的三维问题。通过求解伴随方程,可以一次性计算目标函数和约束函数对所有设计变量的导数,显著提高了计算效率。尽管伴随变量法的实现复杂度较高,但在大型问题中表现出显著的效率优势,为复杂结构的优化设计提供了强有力的工具。
结论
三维动态平衡方程不仅在数学理论中占据重要地位,还在流体力学、地球物理和拓扑优化等跨学科领域展现出广泛的应用前景。通过挂谷猜想的突破,我们看到了这一理论在推动科学和技术进步中的巨大潜力。未来,随着更多跨学科研究的深入,三维动态平衡方程将继续在多个领域发挥其重要作用,为人类探索未知世界提供新的视角和方法。
