改进决策树算法分类优化方法：理论与应用

引言

决策树算法作为数据挖掘中的重要工具，广泛应用于分类问题中。其中，ID3算法因其简单直观的特点，成为研究和应用的热点。然而，ID3算法在处理多值属性时存在一定的局限性。本文将分析ID3算法的原理及其优缺点，并提出一种改进的优化算法。此外，还将探讨如何结合学习-竞争模式解决NP难组合优化问题，展示多学科交叉在算法优化中的潜力。

ID3算法的原理与优缺点

基本原理

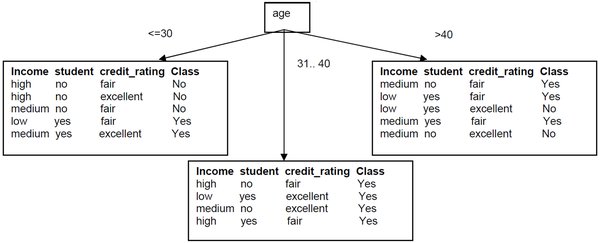
ID3算法是一种基于信息增益的决策树构建方法。其核心思想是通过计算每个属性的信息增益，选择信息增益最大的属性作为当前节点的分裂属性，递归地构建决策树。具体步骤如下：

1. 计算数据集的信息熵。
2. 计算每个属性的信息增益。
3. 选择信息增益最大的属性作为分裂属性。
4. 对每个子集递归执行上述步骤，直到满足终止条件。

优缺点分析

优点

• 简单直观：ID3算法易于理解和实现。
• 高效性：在处理小型数据集时，ID3算法表现出较高的效率。

缺点

• 倾向于多值属性：ID3算法在处理多值属性时，倾向于选择这些属性进行分裂，可能导致决策树过于复杂。
• 过拟合风险：由于ID3算法没有剪枝机制，容易产生过拟合现象。

ID3算法的改进策略

引入参数约束

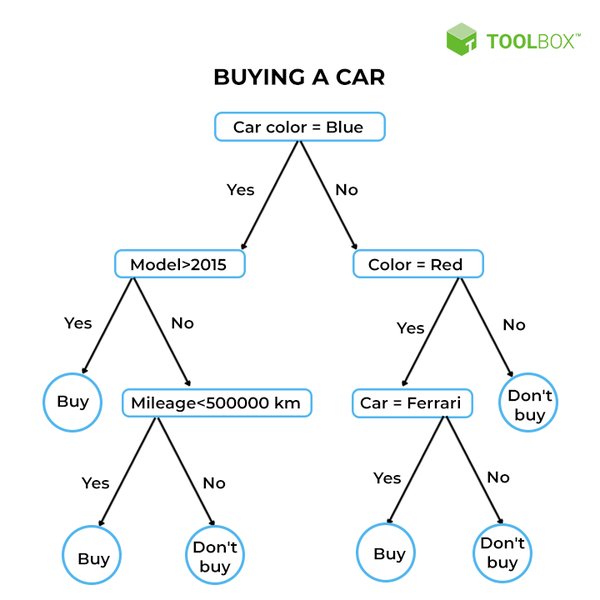
针对ID3算法倾向于多值属性的缺点，本文提出了一种改进算法，通过引入一个参数来约束属性选择。具体步骤如下：

1. 计算数据集的信息熵。
2. 计算每个属性的信息增益。
3. 根据引入的参数，调整信息增益的计算公式，降低多值属性的权重。
4. 选择调整后信息增益最大的属性作为分裂属性。
5. 对每个子集递归执行上述步骤，直到满足终止条件。

优化效果

通过引入参数约束，改进后的ID3算法在处理多值属性时表现出更好的平衡性，减少了决策树的复杂度，降低了过拟合的风险。

学习-竞争模式在组合优化中的应用

模式概述

学习-竞争模式是一种解决NP难组合优化问题的通用模型。其中，“学习模式”侧重于个体局部的搜索，而“竞争模式”侧重于种群全局的搜索。通过将这两种模式结合，可以充分利用不同算法的优点，提高优化效果。

实际应用

以背包问题为例，本文采用贪婪算法实现“学习模式”，遗传算法实现“竞争模式”，并设计了一组参数来协调这两种模式之间的关系。实验结果表明，该模型在解决背包问题时表现出较高的效率和准确性。

多学科交叉在算法优化中的潜力

木材微观结构分析技术

木材是一种多尺度且具有高度各向异性的天然高分子材料，其微观结构对物理力学性能具有重要影响。通过显微观察、X射线照相及衍射分析、计算机断层扫描等技术，可以重建木材微观结构模型，揭示其微观形貌特征。这些技术为算法优化提供了新的思路和方法。

多学科交叉的应用

结合木材微观结构分析技术，可以进一步优化决策树算法。例如，通过模拟木材的微观结构，设计更加复杂的决策树模型，提高分类精度和效率。此外，多学科交叉还可以为其他优化算法提供新的灵感和方法。

结论

本文通过分析ID3算法的优缺点，提出了一种改进的优化算法，并结合学习-竞争模式解决NP难组合优化问题。此外，还探讨了木材微观结构分析技术，展示了多学科交叉在算法优化中的潜力。未来，随着技术的不断进步，决策树算法及其他优化算法将在更多领域得到广泛应用，推动数据挖掘和机器学习的发展。

参考文献

1. 张明靖. 音乐游戏在小学音乐教学中的应用研究[J]. 中国文艺家, 2018(8): 197-199.
2. 徐凤兰. 在音乐中游戏, 在游戏中学习音乐: 议音乐游戏在小学音乐教学中的应用[J]. 北方音乐, 2019, 39(4): 190-193.
3. 陈杰虹. 谈音乐游戏在小学音乐课堂教学中的应用[J]. 试题与研究, 2020(14): 106.
4. 段吉峰. 音乐游戏在小学音乐小班化教学中的应用[J]. 北方音乐, 2020(8): 225-226.
5. 杨瑜婷. 音乐游戏在小学音乐教学中的应用研究[J]. 当代音乐, 2020(1): 60-61.